经典算法之Kruskal算法
一:思想
若存在M={0,1,2,3,4,5}这样6个节点,我们知道Prim算法构建生成树是从”顶点”这个角度来思考的,然后采用“贪心思想”
来一步步扩大化,最后形成整体最优解,而Kruskal算法有点意思,它是站在”边“这个角度在思考的,首先我有两个集合。
1. 顶点集合(vertexs):
比如M集合中的每个元素都可以认为是一个独根树(是不是想到了并查集?)。
2.边集合(edges):
对图中的每条边按照权值大小进行排序。(是不是想到了优先队列?)
好了,下面该如何操作呢?
首先:我们从edges中选出权值最小的一条边来作为生成树的一条边,然后将该边的两个顶点合并为一个新的树。
然后:我们继续从edges中选出次小的边作为生成树的第二条边,但是前提就是边的两个顶点一定是属于两个集合中,如果不是
则剔除该边继续选下一条次小边。
最后:经过反复操作,当我们发现n个顶点的图中生成树已经有n-1边的时候,此时生成树构建完毕。
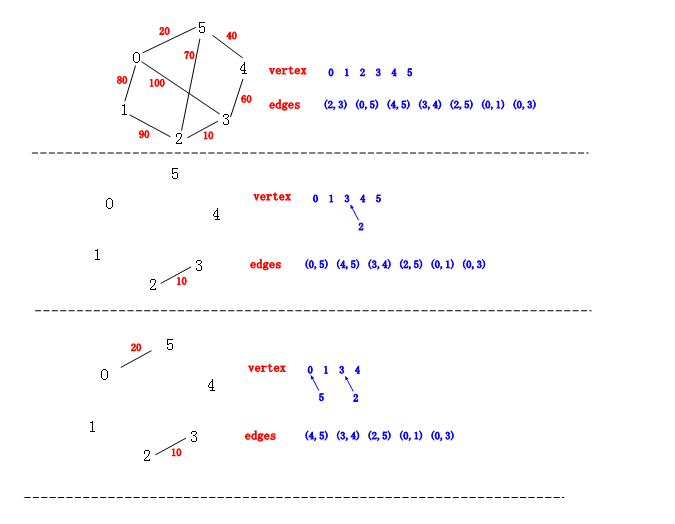
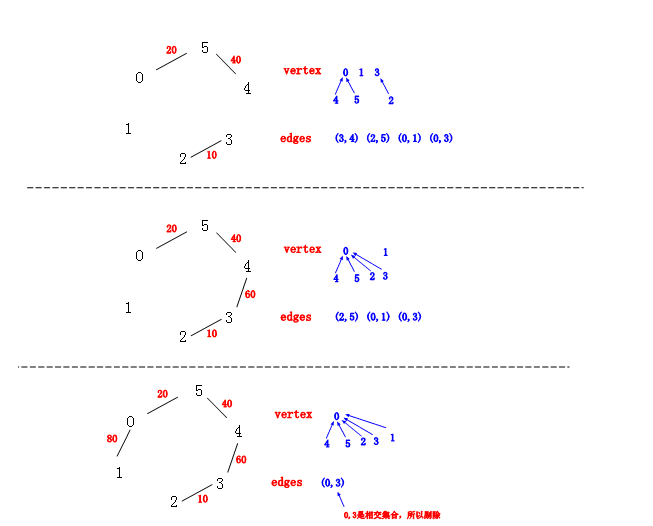
从图中我们还是很清楚的看到Kruskal算法构建生成树的详细过程,同时我们也看到了”并查集“和“优先队列“这两个神器
来加速我们的生成树构建。
二:构建
1.Build方法
这里我灌的是一些测试数据,同时在矩阵构建完毕后,将顶点信息放入并查集,同时将边的信息放入优先队列,方便我们在
做生成树的时候秒杀。
1 #region 矩阵的构建
2 /// <summary>
3 /// 矩阵的构建
4 /// </summary>
5 public void Build()
6 {
7 //顶点数
8 graph.vertexsNum = 6;
9
10 //边数
11 graph.edgesNum = 8;
12
13 graph.vertexs = new int[graph.vertexsNum];
14
15 graph.edges = new int[graph.vertexsNum, graph.vertexsNum];
16
17 //构建二维数组
18 for (int i = 0; i < graph.vertexsNum; i++)
19 {
20 //顶点
21 graph.vertexs[i] = i;
22
23 for (int j = 0; j < graph.vertexsNum; j++)
24 {
25 graph.edges[i, j] = int.MaxValue;
26 }
27 }
28
29 graph.edges[0, 1] = graph.edges[1, 0] = 80;
30 graph.edges[0, 3] = graph.edges[3, 0] = 100;
31 graph.edges[0, 5] = graph.edges[5, 0] = 20;
32 graph.edges[1, 2] = graph.edges[2, 1] = 90;
33 graph.edges[2, 5] = graph.edges[5, 2] = 70;
34 graph.edges[4, 5] = graph.edges[5, 4] = 40;
35 graph.edges[3, 4] = graph.edges[4, 3] = 60;
36 graph.edges[2, 3] = graph.edges[3, 2] = 10;
37
38 //优先队列,存放树中的边
39 queue = new PriorityQueue<Edge>();
40
41 //并查集
42 set = new DisjointSet<int>(graph.vertexs);
43
44 //将对角线读入到优先队列
45 for (int i = 0; i < graph.vertexsNum; i++)
46 {
47 for (int j = i; j < graph.vertexsNum; j++)
48 {
49 //说明该边有权重
50 if (graph.edges[i, j] != int.MaxValue)
51 {
52 queue.Eequeue(new Edge()
53 {
54 startEdge = i,
55 endEdge = j,
56 weight = graph.edges[i, j]
57 }, graph.edges[i, j]);
58 }
59 }
60 }
61 }
62 #endregion2:Kruskal算法
并查集,优先队列都有数据了,下面我们只要出队操作就行了,如果边的顶点不在一个集合中,我们将其收集作为最小生成树的一条边,
按着这样的方式,最终生成树构建完毕,怎么样,组合拳打的爽不爽?
1 #region Kruskal算法
2 /// <summary>
3 /// Kruskal算法
4 /// </summary>
5 public List<Edge> Kruskal()
6 {
7 //最后收集到的最小生成树的边
8 List<Edge> list = new List<Edge>();
9
10 //循环队列
11 while (queue.Count() > 0)
12 {
13 var edge = queue.Dequeue();
14
15 //如果该两点是同一个集合,则剔除该集合
16 if (set.IsSameSet(edge.t.startEdge, edge.t.endEdge))
17 continue;
18
19 list.Add(edge.t);
20
21 //然后将startEdge 和 endEdge Union起来,表示一个集合
22 set.Union(edge.t.startEdge, edge.t.endEdge);
23
24 //如果n个节点有n-1边的时候,此时生成树已经构建完毕,提前退出
25 if (list.Count == graph.vertexsNum - 1)
26 break;
27 }
28
29 return list;
30 }
31 #endregion最后是总的代码:
1 using System;
2 using System.Collections.Generic;
3 using System.Linq;
4 using System.Text;
5 using System.Diagnostics;
6 using System.Threading;
7 using System.IO;
8 using System.Threading.Tasks;
9
10 namespace ConsoleApplication2
11 {
12 public class Program
13 {
14 public static void Main()
15 {
16 MatrixGraph graph = new MatrixGraph();
17
18 graph.Build();
19
20 var edges = graph.Kruskal();
21
22 foreach (var edge in edges)
23 {
24 Console.WriteLine("({0},{1})({2})", edge.startEdge, edge.endEdge, edge.weight);
25 }
26
27 Console.Read();
28 }
29 }
30
31 #region 定义矩阵节点
32 /// <summary>
33 /// 定义矩阵节点
34 /// </summary>
35 public class MatrixGraph
36 {
37 Graph graph = new Graph();
38
39 PriorityQueue<Edge> queue;
40
41 DisjointSet<int> set;
42
43 public class Graph
44 {
45 /// <summary>
46 /// 顶点信息
47 /// </summary>
48 public int[] vertexs;
49
50 /// <summary>
51 /// 边的条数
52 /// </summary>
53 public int[,] edges;
54
55 /// <summary>
56 /// 顶点个数
57 /// </summary>
58 public int vertexsNum;
59
60 /// <summary>
61 /// 边的个数
62 /// </summary>
63 public int edgesNum;
64 }
65
66 #region 矩阵的构建
67 /// <summary>
68 /// 矩阵的构建
69 /// </summary>
70 public void Build()
71 {
72 //顶点数
73 graph.vertexsNum = 6;
74
75 //边数
76 graph.edgesNum = 8;
77
78 graph.vertexs = new int[graph.vertexsNum];
79
80 graph.edges = new int[graph.vertexsNum, graph.vertexsNum];
81
82 //构建二维数组
83 for (int i = 0; i < graph.vertexsNum; i++)
84 {
85 //顶点
86 graph.vertexs[i] = i;
87
88 for (int j = 0; j < graph.vertexsNum; j++)
89 {
90 graph.edges[i, j] = int.MaxValue;
91 }
92 }
93
94 graph.edges[0, 1] = graph.edges[1, 0] = 80;
95 graph.edges[0, 3] = graph.edges[3, 0] = 100;
96 graph.edges[0, 5] = graph.edges[5, 0] = 20;
97 graph.edges[1, 2] = graph.edges[2, 1] = 90;
98 graph.edges[2, 5] = graph.edges[5, 2] = 70;
99 graph.edges[4, 5] = graph.edges[5, 4] = 40;
100 graph.edges[3, 4] = graph.edges[4, 3] = 60;
101 graph.edges[2, 3] = graph.edges[3, 2] = 10;
102
103 //优先队列,存放树中的边
104 queue = new PriorityQueue<Edge>();
105
106 //并查集
107 set = new DisjointSet<int>(graph.vertexs);
108
109 //将对角线读入到优先队列
110 for (int i = 0; i < graph.vertexsNum; i++)
111 {
112 for (int j = i; j < graph.vertexsNum; j++)
113 {
114 //说明该边有权重
115 if (graph.edges[i, j] != int.MaxValue)
116 {
117 queue.Eequeue(new Edge()
118 {
119 startEdge = i,
120 endEdge = j,
121 weight = graph.edges[i, j]
122 }, graph.edges[i, j]);
123 }
124 }
125 }
126 }
127 #endregion
128
129 #region 边的信息
130 /// <summary>
131 /// 边的信息
132 /// </summary>
133 public class Edge
134 {
135 //开始边
136 public int startEdge;
137
138 //结束边
139 public int endEdge;
140
141 //权重
142 public int weight;
143 }
144 #endregion
145
146 #region Kruskal算法
147 /// <summary>
148 /// Kruskal算法
149 /// </summary>
150 public List<Edge> Kruskal()
151 {
152 //最后收集到的最小生成树的边
153 List<Edge> list = new List<Edge>();
154
155 //循环队列
156 while (queue.Count() > 0)
157 {
158 var edge = queue.Dequeue();
159
160 //如果该两点是同一个集合,则剔除该集合
161 if (set.IsSameSet(edge.t.startEdge, edge.t.endEdge))
162 continue;
163
164 list.Add(edge.t);
165
166 //然后将startEdge 和 endEdge Union起来,表示一个集合
167 set.Union(edge.t.startEdge, edge.t.endEdge);
168
169 //如果n个节点有n-1边的时候,此时生成树已经构建完毕,提前退出
170 if (list.Count == graph.vertexsNum - 1)
171 break;
172 }
173
174 return list;
175 }
176 #endregion
177 }
178 #endregion
179 }




